久久精品成人-久久精品成人国产午夜-久久精品成人免费网站-久久精品第一页-亚洲午夜精品aaa级久久久久-亚洲午夜精品一区二区

　　本章主要內容：

　　l認識統計顯著性的實質

　　l理解假設建立的概念及如何檢驗假設

　　l 理解第一類誤差和第二類誤差的區別

　　l 描述幾種常見的統計檢驗方法

　　l方差分析

　　3.1 評估差分和變化

　　測量方法是否有區別是營銷管理人員關心的眾多問題的核心。下面是幾個具體例子：

　　l 我們對認知度所做的事后測試的結果高于事先測試的記錄。是認知度真的提高了，還是另有別的解釋?我們是該終止與代理商的關系還是繼續委托它?

　　l 我們的整體顧客滿意度得分從3個月前的92%上升到今天的93.5%，顧客滿意度真的提高了嗎?我們是否應該慶祝一番?

　　l 采用10點制量表，達拉斯顧客對我們的有線電視系統提供的客戶滿意程度比辛辛那提的平均要高1.2。達拉斯的顧客顧客真的更為滿意么?辛辛那提的顧客服務負責人員是否該被撤換?達拉斯的負責人是否該受到獎勵?

　　l 在最近的一次產品創意調查中，19.8%的被調查者說他們非常可能購買他們評估的新產品。這是否是好事?是否比我們去年對類似產品所做的調查結果要好?這種結果對我們是否推出新產品的決策有何意義?

　　l 在一項市場細分調查中，我們發現年收入30000美圓以上的人去快餐店的次數平均每月為6.2次，而年收入為30000美元或以下的人去的次數為6.7次，這種差別是否真實?是否有意義?

　　l 在一項認知度調查中，28.3%的被調查者在無提示的情況下說知道我們的產品。這是一個好的結果么?

　　以上這些是在營銷調研中永遠存在的問題。盡管被一些人認為枯燥，但它們卻正是統計假設檢驗為什么重要的原因。假設檢驗有助于更接近這些問題的最終答案。我們說接近，是因為在市場調研中很少能完全確定地回答這些問題。

　　3.2 統計顯著性

　　統計推斷最根本的目的是從抽樣調查的結果中歸納出總體的特征。統計推斷的基本信條是，在數學意義上不同的數字在統計學意義上可能并沒有顯著的不同。例如，調查人員要求喝可樂的人蒙上眼睛品嘗兩種不同的可樂并說出自己更喜歡哪一種。結果表明，51%的人傾向于被試驗的一種，49%的人傾向于另一種。這里有一個數學上的差別，但這種差別極小且并不重要。它可能在我們準確判斷自己口味偏好能力的誤差范圍之內，這種差別在統計意義上可能并不顯著。關于差分有三個不同的概念：

　　l 數學差分 根據定義，如果幾個數字不完全相同，它們就有差分。然而，這并不能說明差分的重要性及在統計上的顯著性。

　　l 統計顯著性 如果一個特殊的差分大到不可能是由于偶然因素或抽樣誤差引起的地步，那么這個差分在統計意義上是顯著的

　　l 管理意義上的重要差分 如如果或數字的差異程度從管理角度看是有意義的，那么我們可以說這個差分是重要的。例如，在顧客對兩種不同包裝的反應的調查中，其差分在統計上也許很顯著，但可能小到沒有實際及管理上的重要性。

　　在本章，我們將介紹幾種檢驗結果是否具有統計顯著性的方法。

　　3.3 假設檢驗

　　假設可以定義為一個管理者或管理者對被調查者總體特征所做的一種假定或猜想。營銷人員常常要面臨這樣的問題，即調查結果是否與標準有很大的差別，以便決定公司營銷策略的某些方面是否需要改變。讓我們看看下面幾種情形：

　　l 一項跟蹤調查的結果表明，顧客對產品的了解程度比6個月前所做的類似調查中顯示的要低。結果是否明顯降低?是否低到需要改變廣告策略的程度?

　　l 一位經理認為其產品購買者平均年齡為35歲。為檢驗其假設，他進行了一項調查，調查表明購買者平均年齡為36.5歲。調查結果與其觀點的差別是否足以說明此經理的觀點是不正確的?

　　l 一家快餐店的營銷部長認為她的顧客中60%為女性，40%為男性。為此她進行了一項調查，通過調查她發現顧客55%為女性，45%為男性。調查結果與她原來假設的差別是否足以讓她得出“她原來的假設是錯誤的”這一結論?

　　所有這些問題都可以通過一定的統計檢驗來評估。在假設檢驗中，調查者測定一個關于總體特征的假設是否有根據。如果假設確實正確，統計假設檢驗便可以讓我們計算出一個特殊結果的概率。

　　對于一項具體調查結果與假設值之間的差分有兩種主要的解釋：假設是正確的，差分很可能是因為抽樣的錯誤造成的;或者假設很可能是錯誤的，真正的數值是另外的值。

　　假設檢驗的步驟

　　檢驗一個假設主要有五個步驟。首先必須被明確。其次，選擇適當的統計方法來檢驗假設。第三，判斷標準必須明確，并作為決定是否拒絕或不能拒絕(FTR)原假設H0的基礎。請注意，我們不說“拒絕H0或接受H0”，盡管這看似很細微的區別，但卻很重要。對這一區別我們在后文中進一步論述。第四，計算檢驗統計值并進行檢驗。第五，從初始問題或調查問題的角度陳述結論。

　　1 陳述假設

　　假設主要用兩種形式：原假設H0與備擇假設H1，原假設H0與備擇假設H1在檢驗時是相對的。例如：調研部經理認為他的操作程序將使顧客在汽車購物窗前的等待時間為2分鐘，1000個樣本的平均時間為2.4分鐘，這時，原假設與備擇假設將表示如下：

　　原假設H0：標準等待時間=2分鐘

　　備擇假設H1：標準等待時間¹2分鐘

　　2 選擇適當的檢驗統計量

　　本章將介紹幾種檢驗方法，分析人員必須根據調查情況選擇合適的統計檢驗方法。

　　3 確定判定規則

　　從前面關于樣本均值的討論中可以發現，抽樣結果與總體參數完全相等的情況幾乎是不可能發生的。關鍵的問題是，如果統計假設是正確的，實際樣本平均數和假設平均數間的差分是否會在一個可以接受的范圍。因此，需要一個判斷規則或標準，來決定是否拒絕或不拒絕原假設。統計上用顯著水平來說明判定規則。

　　顯著水平(a)在選擇原假設和備擇假設的過程中是很關鍵的。顯著水平是判定原假設的可接受性時的一種認為很低的概率，如0.10，0.05或0.01。

　　如果我們決定一項顯著水平為0.05的假設，這表示如果由于巧合或抽樣誤差，檢驗表明觀察結果發生的概率為5%，那么我們將拒絕原假設。對原假設的拒絕相等于認同備擇假設。

　　4 計算統計檢驗值

　　在這一步驟中，要求：

　　l 運用適當的公式計算統計檢驗值

　　l 比較計算值與根據判定規則所得的嚴格的統計值(從適當的統計表格中查得)

　　l通過比較，得出是否拒絕原假設H0的結論

　　5 表述結果

　　從初始研究問題的角度表述你的結論，以總結檢驗結果。

　　3.4 假設檢驗中的兩類錯誤

　　假設檢驗中容易犯兩種錯誤類型，一般稱之為第一類錯誤和第二類錯誤。第一類錯誤發生在如下情形：調查者拒絕了原假設，而實際上它是正確的。調查得出的這種不正確的結論也許是由于樣本與總體值的差分是由于抽樣誤差造成的。調查者必須決定在多大程度上認同第一類錯誤。認同第一類錯誤的可能性被認為是a水平。相反地，如果在它事實上正確的時候，我們沒有拒絕它，那么1-a將是得出正確結論的概率。

　　第二類錯誤發生在如下情形：原假設錯誤，而調查者沒有拒絕它。第二類錯誤被認為是b錯誤，1-b的值，反映了在原假設錯誤的時候，作出正確決定拒絕它的概率。這些不同的概率總結于表3.1中

　　表3.1 第一類錯誤和第二類錯誤

　　然而，對b的估計更為復雜，且已超出我們討論的范圍。并且，第一類錯誤與第二類錯誤并不是互補的，即

　　對于任何假設檢驗，我們都希望能控制n(樣本容量)、a(第一類錯誤)及b(第二類錯誤)。遺憾的是，這三個量中我們只能控制兩個。對于一個規定了樣本量的問題，n是固定的，因此，a與b只能控制一個。

　　3.5 假設檢驗方法

　　本章將介紹最常用的檢驗和t檢驗

　　3.5.1 t檢驗

　　(1) t分布的背景

　　從均數為m、標準差為s的正態分布總體中，隨機抽取一個含量為n的樣本，樣本均數為，

　　理論證明：服從均數為、標準差為的正態分布，對其進行標準化，表達式的正態分布，對其進行標準化服從標準正態分布，由于s未知，用樣本標準差S代替，表達式，表達式所服從的分布即為t分布。

　　(2) t分布的特點

　　t分布類似于標準正態分布，以0為中心，左右兩側對稱，中間面積大，兩側面積小，象一個‘鐘型’曲線，曲線下的面積為1，理論證明，當樣本含量趨向無窮時，t分布即為標準正態分布。

　　對任意給定的概率a，總對應一個點，在這個點的左側的面積為a/2，這個點，在統計學上稱為界點，常用表示，即從至，包含了總體1-a的個體，a常取值0.05、0.01。

　　(3) t檢驗的基本思想

　　有一個服從正態分布的總體，研究者想知道總體均數是否為m0，于是從中隨機抽取一個樣本，若總體均數為m0，不妨取a=0.05，則服從t分布，t值應位于，否則，有理由懷疑總體均數為。

　　(4) t檢驗的基本步驟

　　第一步 建立假設并確定檢驗水準

　　假設有兩種：1)檢驗假設H0(hypothesis to be tested)

 

　　2)備擇假設H1(alternative hypothesis)

　　常取a=0.05或a=0.01

　　第二步 選定統計方法，計算統計量

　　第三步 確定P值和作出推斷結論

　　如,則

　　，認為H0不成立，否則，不拒絕H0。

　　(5)實例

　　某媒體報道：2000年廣州居民家庭平均總收入為3.6萬元，報道是否正確?某調查公司隨機調查了20個家庭，數據如下(單位：萬元)：2.3、3.8、4.5、3.3、3.5、5.6、4.3、6.2、2.8、5.2、3.2、3.8、4.8、3.2、3.9、4.6、4.5、5.2、3.8、5.5

　　經計算： ，S=1.02，n=20

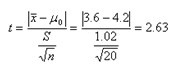
　　查t界值表t0.05(20-1)=2.093，t>t0.05(20-1)，P<0.05，可以認為，廣州市居民的年平均總收入不是3.6萬元。

　　(6) t檢驗的基本類型

　　t檢驗常用于以下3種情況

　　(a) 樣本均數與總體均數比較的t檢驗

　　(b) 兩樣本均數比較的t檢驗

　　檢驗假設，備擇假設

　　統計量為：

　　自由度n=n1+n2-2

　　其中，

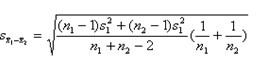
　　(c) 配對設計的t檢驗

　　3.5.2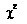檢驗

　　基本思想

　　舉例說明，調研部經理對廣州、北京兩城市居民進行了電話訪問，樣本量分別為110、105。廣州100名被訪者中，60名使用該公司洗頭水，40名使用其他廠家產品;北京100被訪者總52名使用公司洗發水，48名使用其他廠家產品，調研部經理需要判斷，該公司在兩城市的洗發水市場的占有率是否相同。現將資料整理成如下形式：

　　表3.2 甲、乙兩地某品牌洗發水使用情況

　　表中，A11、A12、A21、A22這四個格子的數據是整個表的基本數據，其余數據都是從這四個基本數據推算而來，因而，稱該表為四格表。我們想了解，廣州、北京該公司的占有率是否相同?經計算，廣州樣本率為P1=59.1%;北京為P2=46.7%，廣州、北京兩地的樣本率不同，這個不同是由兩地總體率不同造成的?還是僅由抽樣誤差造成的?下面進行假設檢驗

　　檢驗步驟為：

，即兩地該公司占有率相同

，即兩地占有率不相同

　　顯著水平a取0.05，由相應表格查得，界值為3.84

        統計方法，選用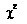檢驗，公式為：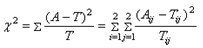

　　其中Aij為實際數，Tij為理論數，計算公式為

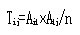
　　本例計算如下：T11=121x110/215=61.9，同理可計算T12=110-61.5=48.1，T21=59.1，T22=45.9，代入公式，可得：

　　由相應表格查得，a=0.05時

　　界值為3.84，由此可得出P<0.05

　　結論：P1與P2的差分按0.05的顯著水平屬于抽樣誤差，不拒絕H0，認為該公司在廣州、北京的占有率相同。

　　3.6 方差分析

　　方差分析(Analysis of Variance，簡稱ANOVA)是一種對多個樣本均數進行分析比較的統計方法，其基本原理是：指標的總變異又類別間的變異與隨機變異組成，通過分析總變異的構成，推斷各類別總體均數是否相同。

　　若需要檢驗兩個或兩個以上獨立樣本平均數的差異，方差分析(ANOVA)是一種合適的統計工具。雖然它可以用來檢驗兩個平均數的差異，但是它更主要地是用于對3個或3個以上獨立群體的平均數差異的假設檢驗。可以用方差分析確定樣本之間平均數的差異是否由抽樣誤差而引致的。上面論及的t檢驗可用于只涉及兩個樣本平均數時的檢驗假設，當有3個或3個以上樣本時，利用這兩種方法缺乏效率。例如，如有5個樣本及相應的平均，那么就需10次t檢驗來檢測每一對平均數。值得注意的是，當有3個或更多個平均數出現時，使用Z檢驗或t檢驗，也增加了出現每類錯誤的可能性。每兩個不同平均數的組合都必須被檢驗。檢驗的次數越多，夸大一對(或更多對)平均數真正由于抽樣誤差引起顯著差異的機會就越大。若顯著性水平為0.05，平均在20次檢驗中就會出現一次。

　　單向方差分析經常被用來分析實驗結果。例如，一家汽車配件連鎖店的市場總經理正在考慮采用三種可能的服務來促銷：車輪校正、換油、調試。她想知道這三種方法帶來的潛在銷售量是存在顯著差異。

　　在3個城市中共隨機出60家連鎖店(每個城市選 20家)，每個城市分別增加一項服務，實驗期間的價格和廣告等保持一致。實驗共進行30天，其間的銷售情況將逐一記錄。

　　表15-6快步示了每家店的平均銷售額。問題是，引起這些差異的主要原因是促銷方式還是純屬偶然?

　　3.6.1 基本統計指標

　　(1) 總變異

　　統計量是總的離均差平方和，用SS總表示，假定共有k個類別，每類分別有ni(i=1,2,…,k)個個體，公式為：

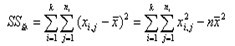
　　其中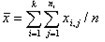，，自由度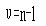

　　(2) 組間變異

　　組間變異為：

　　組間均方變異為：

 

 

　　其中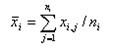，(i=1,2,…,k) ，自由度

　　(3) 組內變異

　　組內變異為：

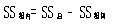
　　組間均方變異為：

　　其中，自由度

　　方差分析的基本思想是：當各類別總體均數相同時，間的差異

　　由隨機誤差造成，與

　　的比值應接近1，當其比值大于1、并超出一定的范圍時，可以認為各類別間的總體均數不全相等、存在差異。

　　3.6.2 統計量

　　(1)整體均數比較

　　對各類別均數整體方面的檢驗，統計量為：

　　　　由分子自由度為、分母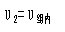、顯著水平a，查方差分析專用F界值表，得界值，統計量F與界值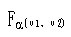

　　比較，若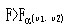,P<0.05，可以認為不同類別的總體均數不全相同，需進一步對兩兩間的情況進行檢驗，否則，P>0.05，認為各類總體均數相同。

　　(2) 兩兩比較

　　市場研究中，多個樣本均數間的兩兩比較(稱為多重比較，multiple comparison)，常采用q檢驗(Newman-Keuls method，SPSS中用S-N-K法)，統計量為：

q界值除與顯著水平a有關外，還與分子、分母自由度有關，分子自由度等于A類與B類間的類別數a與分母自由度為誤差自由度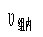。分子自由度a的計算方法是，將每類樣本均數按從小到大的順序排列，a=A類的序號-B類的序號+1。

　　3.6.3 實例

　　為評估某行業職工收入情況，調查三地該行業職工各6人，結果見下表。

　　表1 三地某行業18名職工年收入表(萬元)

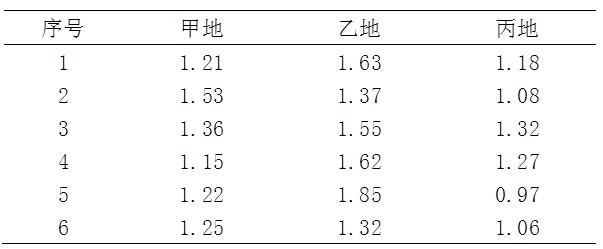
　　(1) 統計描述

　　

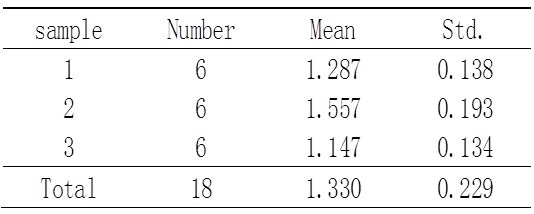
(2) F檢驗

　

　界值F0.05(2,15)=3.68，P<0.05，可以認為三地平均工資有差異。

　　(3) q檢驗

　　

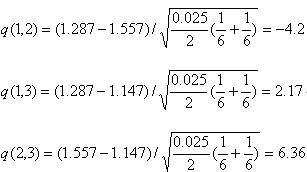
        按均數大小排列，(1)類別3，(2)類別1，(3)類別2，所以，a(1,2)=2,a(1,3)=2,a(2,3)=3

　　顯著水平取0.05，查q界值表， q0.05(2,15)=3.01, q0.05(3,15)=3.67，經比較，可以認為甲、丙地區間無差別，乙與甲、乙與丙間有差異。

上一篇下一篇